1.
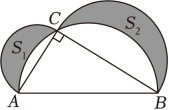
如图,阴影部分表示以Rt△ABC的各边为直径的三个半圆所组成的两个新月形,面积分别记作S1和S2 . 若AC=6,BC=8,则阴影部分面积S1+S2是( )
A.
9π
B.
12.5π
C.
14
D.
24
【考点】
勾股定理;
几何图形的面积计算-割补法;
基础巩固
能力提升
变式训练
拓展培优
真题演练