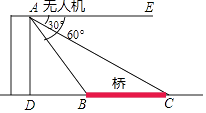
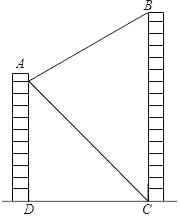
如图，热气球的探测器显示，从热气球A处看一栋楼顶部B的仰角为，看这栋楼底部C的俯角为，热气球A处与楼的水平距离为m米，那么这栋楼的高度为米．（用含的式子表示）

1. 如图，热气球的探测器显示，从热气球A处看一栋楼顶部B的仰角为 $\text{[math]}$ ，看这栋楼底部C的俯角为 $\text{[math]}$ ，热气球A处与楼的水平距离为m米，那么这栋楼 $\text{[math]}$ 的高度为米．（用含 $\text{[math]}$ 的式子表示）

【考点】

解直角三角形的实际应用﹣仰角俯角问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

填空题容易

1. 如图，一款可调节的笔记本电脑支架放置在水平桌面上，调节杆 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 的最大仰角为a．当 $\text{[math]}$ 时，则点A到桌面的最大高度是

填空题容易

2. 如图，鹿鸣公园要从A地向B地修一条隧道（点A、B在同一水平线上）．为了测量A、B两地之间的距离，一架无人机从A地出发，垂直上升50米到达C处，在C处观察B地的俯角α为30°，则A、B两地之间的距离为米．（结果保留根号）

填空题容易

3. 某防空部队进行射击训练时．在地面 $\text{[math]}$ ， $\text{[math]}$ 两个观察点测得空中固定目标 $\text{[math]}$ 的仰角为 $\text{[math]}$ 和 $\text{[math]}$ ，测得 $\text{[math]}$ $\text{[math]}$ 则目标 $\text{[math]}$ 距离地面的高度为 $\text{[math]}$ ．

填空题容易