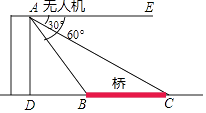
1.
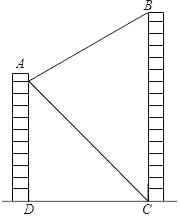
如图,两座建筑物  与
与  ,其中
,其中  的高为120米,从
的高为120米,从  的顶点
的顶点  测得
测得  顶部
顶部  的仰角为30°,测得其底部
的仰角为30°,测得其底部  的俯角为45°,求这两座建筑物的地面距离
的俯角为45°,求这两座建筑物的地面距离  为多少米?(结果保留根号)
为多少米?(结果保留根号)
【考点】
解直角三角形的实际应用﹣仰角俯角问题;