1.
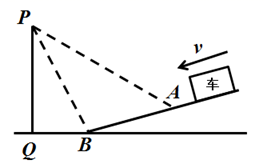
河南省洛阳市应天门是隋唐洛阳城·宫城——紫微城的正南门,俗称五凤楼.应天门是一座由门楼、朵楼和东西阙楼及其间的廊庑为一体的“凹”字形巨大建筑群,两侧的阙高的高度相同,被称为“天下第一门”.某校数学兴趣小组要测量应天门两侧的阙高的高度,如图,他们在点 处测得应天门两侧的阙的最高点
处测得应天门两侧的阙的最高点 的仰角为
的仰角为 , 再往应天门两侧阙高方向前进
, 再往应天门两侧阙高方向前进 至点
至点 处,测得应天门两侧阙的最高点
处,测得应天门两侧阙的最高点 的仰角为
的仰角为 , 根据这个兴趣小组测得的数据,计算应天门两侧阙高
, 根据这个兴趣小组测得的数据,计算应天门两侧阙高 的高度.(结果精确到
的高度.(结果精确到 , 参考数据:
, 参考数据: ,
,  ,
,  )
)

【考点】
解直角三角形的实际应用﹣仰角俯角问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练