1.
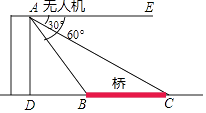
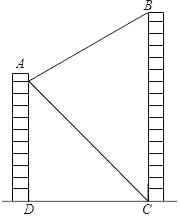
某学校数学探究小组利用无人机在操场上开展测量教学楼高度的活动.如图,此时无人机在离地面20 m的点A处,无人机测得教学楼底部B处的俯角为53°,测得教学楼顶部C处的俯角为30°.求教学楼 的高(结果保留一位小数.参考数据:
的高(结果保留一位小数.参考数据: . )
. )

【考点】
解直角三角形的实际应用﹣仰角俯角问题;