1.
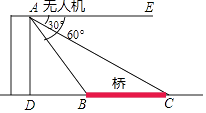
综合实践活动中,数学兴趣小组利用无人机测量大楼的高度.如图,无人机在离地面40米的D处,测得操控者A的俯角为 , 测得楼
, 测得楼 楼顶C处的俯角为
楼顶C处的俯角为 , 又经过人工测量得到操控者A和大楼
, 又经过人工测量得到操控者A和大楼 之间的水平距离是80米,则楼
之间的水平距离是80米,则楼 的高度是多少米?(点A , B , C , D都在同一平面内,参考数据:
的高度是多少米?(点A , B , C , D都在同一平面内,参考数据: )
)

【考点】
解直角三角形的实际应用﹣仰角俯角问题;