1.
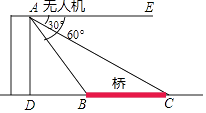
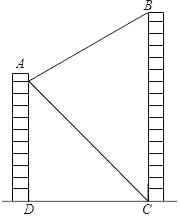
如图是甲、乙两栋居民楼,小明在甲居民楼的楼顶D处观测乙居民楼楼底B处的俯角是45°,观测乙居民楼楼顶A处的仰角为30°,已知甲居民楼的高为16m,求乙居民楼的高是多少?(参考数据: ≈1.41,
≈1.41, ≈1.73,结果精确到0.1m)
≈1.73,结果精确到0.1m)

【考点】
解直角三角形的实际应用﹣仰角俯角问题;