1.
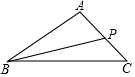
如图,在△ABC中,点P是AC上一点,连接BP,求作一点M,使得点M到AB和AC两边的距离相等,并且到点B和点P的距离相等.(不写作法,保留作图痕迹)
【考点】
角平分线的性质;
线段垂直平分线的性质;
尺规作图-作角的平分线;
尺规作图-垂直平分线;
基础巩固
能力提升
变式训练
拓展培优
真题演练