1.
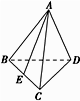
在空间四边形ABCD中,AB=CD , AB与CD成30°角,E , F分别为BC , AD的中点,求EF与AB所成的角.
【考点】
异面直线所成的角;
基础巩固
能力提升
变式训练
拓展培优
真题演练