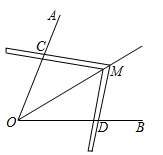
工人师傅常用直角尺平分一个角，做法如下：如图所示，在的边，上分别取，移动直角尺，使直角尺两边相同的刻度分别与，重合（即）．此时过直角尺顶点的射线即是的平分线．这种做法的道理是（）

1. 工人师傅常用直角尺平分一个角，做法如下：如图所示，在 $\text{[math]}$ 的边 $\text{[math]}$ ， $\text{[math]}$ 上分别取 $\text{[math]}$ ，移动直角尺，使直角尺两边相同的刻度分别与 $\text{[math]}$ ， $\text{[math]}$ 重合（即 $\text{[math]}$ ）．此时过直角尺顶点 $\text{[math]}$ 的射线 $\text{[math]}$ 即是 $\text{[math]}$ 的平分线．这种做法的道理是（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

【考点】

三角形全等的判定-SSS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题容易

1. 如图，用直尺和圆规作∠AOB的平分线OC，则△DOC≌△EOC的依据是（）

A. SSS B. SAS C. ASA D. AAS

单选题容易

2. 如图，在 $\text{[math]}$ 和 $\text{[math]}$ 中， $\text{[math]}$ ，还需添加两个条件才能使 $\text{[math]}$ ，添加的一组条件不正确的是（）

A. $\text{[math]}$ ， $\text{[math]}$ B. $\text{[math]}$ ， $\text{[math]}$ C. $\text{[math]}$ ， $\text{[math]}$ D. $\text{[math]}$ ， $\text{[math]}$

单选题容易

3. 如图，用直尺和圆规作∠A^'O^'B^'=∠AOB，能够说明作图过程中△C^'O^'D^'≌△COD的依据是（　　）

A. 角角边 B. 角边角 C. 边角边 D. 边边边

单选题容易