1.
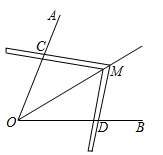
如图是雨伞在开合过程中某时刻的截面图,伞骨AB=AC , 点D , E分别是AB , AC的中点,DM , EM是连接弹簧和伞骨的支架,且DM=EM , 已知弹簧M在向上滑动的过程中,总有△ADM≌△AEM , 其判定依据是( )

A.
SSS
B.
SAS
C.
ASA
D.
HL
【考点】
三角形全等的判定-SSS;