1.
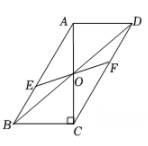
如图,已知抛物线y=﹣x2+bx+c经过点A(﹣1,0),B(3,0),与y轴交于点C,点P是抛物线上一动点,连接PB,PC.
(1)求抛物线的解析式;
(2)如图1,当点P在直线BC上方时,过点P作PD上x轴于点D,交直线BC于点E.若PE=2ED,求△PBC的面积;
(3)抛物线上存在一点P,使△PBC是以BC为直角边的直角三角形,求点P的坐标.

【考点】
二次函数的实际应用-几何问题;