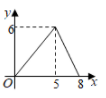
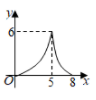
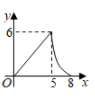
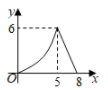
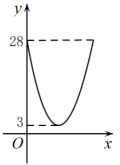
如图，用绳子围成周长为的矩形，记矩形的一边长为，矩形的面积为．当x在一定范围内变化时，S随x的变化而变化，则S与x满足的函数表达式为（）

1. 如图，用绳子围成周长为 $\text{[math]}$ 的矩形，记矩形的一边长为 $\text{[math]}$ ，矩形的面积为 $\text{[math]}$ ．当x在一定范围内变化时，S随x的变化而变化，则S与x满足的函数表达式为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

【考点】

二次函数的实际应用-几何问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题容易

1. 抛物线 $\text{[math]}$ 与 $\text{[math]}$ 轴交于A、B，与 $\text{[math]}$ 轴交于C点，则△ABC的面积为（）

A. 3 B. 4 C. 10 D. 12

单选题容易

2. 园林部门计划在某公园建一个长方形苗圃 $\text{[math]}$ ，苗圃的一面靠墙（墙最大可用长度为 $\text{[math]}$ 米），另三边用木栏围成，中间也用垂直于墙的木栏隔开，分成两个区域，并各留 $\text{[math]}$ 米宽的门（门不用木栏），若建成后所用木栏总长为 $\text{[math]}$ 米，则长方形 $\text{[math]}$ 的最大面积为（）

A. $\text{[math]}$ 平方米 B. 108平方米 C. $\text{[math]}$ 平方米 D. $\text{[math]}$ 平方米

单选题容易

3. 小明以二次函数 $\text{[math]}$ 的图象为模型设计了一款杯子，如图为杯子的设计稿，若 $\text{[math]}$ ， $\text{[math]}$ ，则杯子的高CE为（）

A. 21 B. 22 C. 23 D. 24

单选题容易