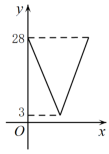1.
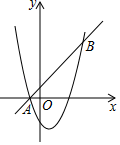
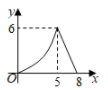
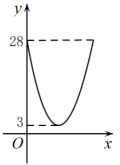
为了美观,在加工太阳镜时将下半部分轮廓制作成抛物线的形状(如图所示),对应的两条抛物线关于 轴对称,
轴对称, 轴,
轴, , 最低点
, 最低点 在
在 轴上,高
轴上,高 ,
,  , 则右轮廍
, 则右轮廍 所在抛物线的解析式为.
所在抛物线的解析式为.

【考点】
二次函数的实际应用-几何问题;
基础巩固
能力提升
变式训练
拓展培优
真题演练