1.
【问题背景】
已知抛物线(a,b为常数,
)的顶点为
, 对称轴与
轴相交于点
, 点
在抛物线上,
为坐标原点.
【构建联系】
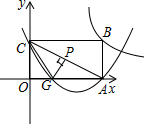
(1)如图1,当 , 与
交于点
时,求该抛物线顶点
的坐标;
(2)如图2,当时,求
的值;
【深入探究】
(3)如图3,若是抛物线上的点,且点
在第四象限,
,
, 点
在线段
上,点
在线段
上,
, 当
取得最小值为
时,求
的值.
【考点】
待定系数法求二次函数解析式;
勾股定理;
基础巩固
能力提升
变式训练
拓展培优
真题演练