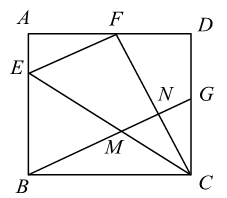
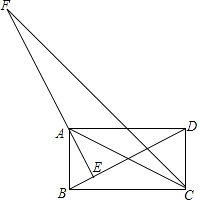
折纸是--种常见的游戏，九年级兴趣小组以“矩形的折叠”为主题开展数学活动．（1）操作判断如图1，在矩形纸片中，，首先沿过点B的直线翻折，使点A落在边上的点E处，折痕为，连接；此时，就可以得到一个四边形，则四边形的形状是哪种特殊的四边形?答：______．（2）深入探究继续沿过点E的直线翻折，使点C落在边上的点G处，折痕为，连接，，延长交于点M，连接． ①的度数为______；②猜想线段和的数量关系，并证明：拓展应用延长交矩形的边于点N，若，，直接写出的值．

1. 折纸是--种常见的游戏，九年级兴趣小组以“矩形的折叠”为主题开展数学活动．

（1）操作判断

如图1，在矩形纸片 $\text{[math]}$ 中， $\text{[math]}$ ，首先沿过点B的直线翻折，使点A落在 $\text{[math]}$ 边上的点E处，折痕为 $\text{[math]}$ ，连接 $\text{[math]}$ ；此时，就可以得到一个四边形 $\text{[math]}$ ，则四边形 $\text{[math]}$ 的形状是哪种特殊的四边形?答：______．

（2）深入探究

继续沿过点E的直线翻折，使点C落在 $\text{[math]}$ 边上的点G处，折痕为 $\text{[math]}$ ，连接 $\text{[math]}$ ， $\text{[math]}$ ，延长 $\text{[math]}$ 交 $\text{[math]}$ 于点M，连接 $\text{[math]}$ ．

① $\text{[math]}$ 的度数为______；

②猜想线段 $\text{[math]}$ 和 $\text{[math]}$ 的数量关系，并证明：

拓展应用

延长 $\text{[math]}$ 交矩形 $\text{[math]}$ 的边于点N，若 $\text{[math]}$ ， $\text{[math]}$ ，直接写出 $\text{[math]}$ 的值．

【考点】

矩形的性质; 相似三角形的判定与性质;

【答案】

您现在未登录，无法查看试题答案与解析。登录

证明题困难

1. 如图，四边形 $\text{[math]}$ 是 $\text{[math]}$ 的内接矩形， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则矩形 $\text{[math]}$ 的周长是 $\text{[math]}$ ．

填空题容易

2. 如图，一块材料的形状是锐角 $\text{[math]}$ ，边 $\text{[math]}$ ，高 $\text{[math]}$ ．把它加工成正方形零件，使正方形的一边在 $\text{[math]}$ 上，其余两个顶点分别在 $\text{[math]}$ 上，求这个正方形零件的边长是多少？

解答题容易

3. 如图，D是△ABC的边AC上的一点，连接BD，已知∠ABD=∠C，AB=6，AD=4，求线段CD的长．

解答题容易