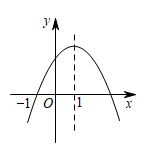已知抛物线与x轴有两个不同的交点．(1) 求c的取值范围；(2) 抛物线与x轴两交点的距离为2，求c的值．

1. 已知抛物线 $\text{[math]}$ 与x轴有两个不同的交点．

(1) 求c的取值范围；

(2) 抛物线 $\text{[math]}$ 与x轴两交点的距离为2，求c的值．

【考点】

二次函数图象与坐标轴的交点问题; 二次函数与一元二次方程的综合应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 二次函数 $\text{[math]}$ 的图象如图所示，若关于x的一元二次方程 $\text{[math]}$ 有两个不相等的实数根，则整数m的最小值为．

填空题容易

2. 抛物线 $\text{[math]}$ 与x轴正半轴交点的坐标为．

填空题容易

3. 抛物线 $\text{[math]}$ 与y轴的交点坐标为．

填空题容易