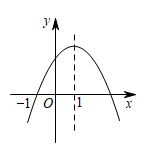已知二次函数．

1. 已知二次函数 $\text{[math]}$ ．

(1) 求函数图象与x轴的公共点的个数；

(2) 若 $\text{[math]}$ ， $\text{[math]}$ $\text{[math]}$ 在二次函数图象上，试比较 $\text{[math]}$ 与 $\text{[math]}$ 的大小．

【考点】

二次函数图象与坐标轴的交点问题; 二次函数与一元二次方程的综合应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 已知抛物线 $\text{[math]}$ 与x轴有两个不同的交点．

(1) 求c的取值范围；

(2) 抛物线 $\text{[math]}$ 与x轴两交点的距离为2，求c的值．

解答题普通

2. 我国著名数学家华罗庚曾说过：“数与形，本是相倚依，焉能分作两边飞．数缺形时少直观，形少数时难入微；数形结合百般好，割裂分家万事非．切莫忘，几何代数统一体，永远联系，切莫分离！”数形结合是解决数学问题的重要思想方法．请结合所学的数学解决下列问题．

在平面直角坐标系中，若点的横坐标、纵坐标都为整数，则称这样的点为整点．

设函数 $\text{[math]}$ （实数 $\text{[math]}$ 为常数）的图象为图象 $\text{[math]}$ ．

(1) 求证：无论 $\text{[math]}$ 取什么实数，图象 $\text{[math]}$ 与 $\text{[math]}$ 轴总有公共点；

(2) 是否存在非负整数 $\text{[math]}$ ，使图象 $\text{[math]}$ 与 $\text{[math]}$ 轴的公共点都是整点？若存在，求所有非负整数 $\text{[math]}$ 的值；若不存在，请说明理由．

解答题困难

3. 已知抛物线y=ax²+x+1（ $\text{[math]}$ ）

(1) 若抛物线的图象与x轴只有一个交点，求a的值；

(2) 若抛物线的顶点始终在x轴上方，求a的取值范围．

解答题普通