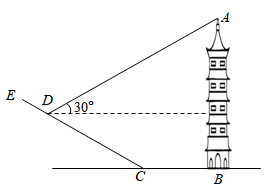
高铁沙坪坝站双子塔为国内首例在高铁站上实施商业开发的综合体．如图，小南在与塔底同一高度的地面处测得塔顶的仰角为．接下来，他沿一条坡比为1：2.4的斜坡行进了156米后，在处测得塔顶的仰角为，点在同一平面内，则小南测得的双子塔的高度约为（）米．（参考数据：，，）

1. 高铁沙坪坝站双子塔为国内首例在高铁站上实施商业开发的综合体．如图，小南在与塔底 $\text{[math]}$ 同一高度的地面 $\text{[math]}$ 处测得塔顶 $\text{[math]}$ 的仰角为 $\text{[math]}$ ．接下来，他沿一条坡比为1：2.4的斜坡 $\text{[math]}$ 行进了156米后，在 $\text{[math]}$ 处测得塔顶 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，点 $\text{[math]}$ 在同一平面内，则小南测得的双子塔 $\text{[math]}$ 的高度约为（）米．（参考数据： $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ）

A. 193 B. 196 C. 201 D. 206

【考点】

解直角三角形的实际应用﹣坡度坡角问题; 解直角三角形的实际应用﹣仰角俯角问题;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题困难

1. 如图，考古队在 $\text{[math]}$ 处测得古塔 $\text{[math]}$ 顶端 $\text{[math]}$ 的仰角为 $\text{[math]}$ ，斜坡 $\text{[math]}$ 的长为 $\text{[math]}$ 米，坡度 $\text{[math]}$ ， $\text{[math]}$ 长为 $\text{[math]}$ 米，则古塔 $\text{[math]}$ 的高度为（）

A. $\text{[math]}$ 米 B. $\text{[math]}$ 米 C. $\text{[math]}$ 米 D. $\text{[math]}$ 米

单选题容易

2. 如图，将一个 $\text{[math]}$ 形状的楔子从木桩的底端点P沿水平方向打入木桩底下，可以使木桩向上运动．若楔子斜面的倾斜角为 $\text{[math]}$ ，楔子沿水平方向前进5厘米，则木桩上升（）

A. $\text{[math]}$ 厘米 B. $\text{[math]}$ 厘米 C. $\text{[math]}$ 厘米 D. $\text{[math]}$ 厘米

单选题容易

3. 如图，小明在点 $\text{[math]}$ 处测得树的顶端 $\text{[math]}$ 仰角为 $\text{[math]}$ ，同时测得 $\text{[math]}$ ，则树的高度 $\text{[math]}$ 为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易