1.
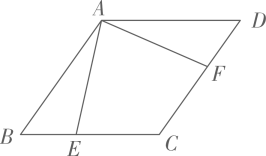
如图,菱形ABCD中,过点C分别作边AB,AD上的高CE,CF,求证:BE=DF.

【考点】
三角形全等及其性质;
菱形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练