1.
如图,池塘两端A、B的距离无法直接测量,请同学们设计测量A、B之间距离的方案.

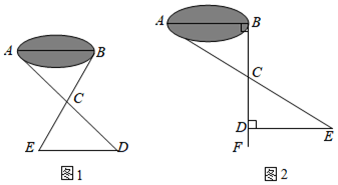
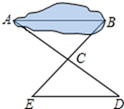
小明设计的方案如图①:他先在平地上选取一个可以直接到达A、B的点O,然后连接AO和BO,接着分别延长AO和BO并且使CO=AO,最后连接CD,测出CD的长即可.
小红的方案如图②:先确定直线AB,过点B作AB的垂线BE,在BE上选取一个可以直接到达点A的点D,在线段AB的延长线上找一点C,使DC=DA
你认为以上两种方案可以吗?请说明理由.
【考点】
全等三角形的应用;
基础巩固
能力提升
变式训练
拓展培优
真题演练