1.
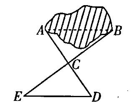
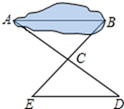
如图,有一池塘  要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C , 连接AC并延长到D , 使
要测池塘两端A、B的距离,可先在平地上取一个可以直接到达A和B的点C , 连接AC并延长到D , 使  连接BC并延长到E , 使
连接BC并延长到E , 使  连接DE , 那么量出DE的长,就是A、B的距离
连接DE , 那么量出DE的长,就是A、B的距离  请说明DE的长就是A、B的距离的理由.
请说明DE的长就是A、B的距离的理由.
【考点】
全等三角形的应用;