1.
如图,在 的方格纸中,每个小正方形的边长为
的方格纸中,每个小正方形的边长为 ,
,  ,
,  ,
,  ,
,  ,
,  均为格点,
均为格点, ,
,  交于点
交于点 , 过
, 过 ,
,  ,
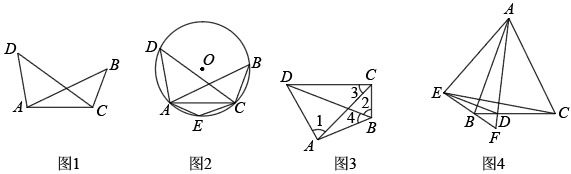
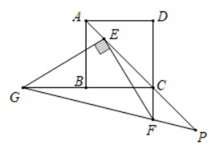
,  三点的圆如图所示,请利用无刻度直尺找出该圆的圆心
三点的圆如图所示,请利用无刻度直尺找出该圆的圆心 , 并简要说明点
, 并简要说明点 的位置是如何找到的
的位置是如何找到的 不要求证明
不要求证明 .
.

【考点】
圆周角定理;
确定圆的条件;
基础巩固
能力提升
变式训练
拓展培优
真题演练