1.
如图,以直角三角形的各边为边向外作正方形,再把较小的两个正方形放置在最大的正方形内,若知道图中阴影部分的面积,则一定能求出哪个图形的面积( )
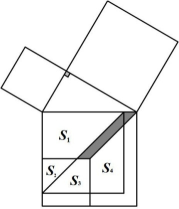
A.
S1
B.
S2
C.
S3
D.
S4
【考点】
正方形的性质;
几何图形的面积计算-割补法;