1.
将两张全等的矩形纸片和另两张全等的正方形纸片按如图方式不重叠地放置在矩形ABCD内,其中矩形纸片和正方形纸片的周长相等.若知道图中阴影部分的面积,则一定能求出( )
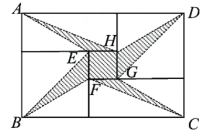
A.
正方形纸片的面积
B.
四边形EFGH的面积
C.
△BEF的面积
D.
△AEH的面积
【考点】
矩形的性质;
正方形的性质;
几何图形的面积计算-割补法;