1.
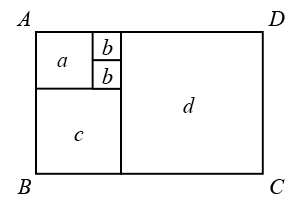
将一个大矩形按如图所示的方式分割成九个小矩形,且只有标号为①和②的两个小矩形为正方形.在满足条件的所有分割中,若知道九个小矩形中 个小矩形的周长,就一定能算出这个大矩形的面积,则
个小矩形的周长,就一定能算出这个大矩形的面积,则 的最小值是( )
的最小值是( )

A.
3
B.
4
C.
5
D.
6
【考点】
矩形的性质;
正方形的性质;