1.
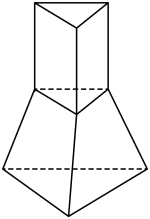
鲁班锁是我国传统的智力玩具,起源于中国古代建筑中的榫卯结构,其内部的凹凸部分啮合十分精巧.图1是一种鲁班锁玩具,图2是其直观图.它的表面由八个正三角形和六个正八边形构成,其中每条棱长均为 . 若该玩具可以在一个正方体内任意转动(忽略摩擦),则此正方体表面积的最小值为.
. 若该玩具可以在一个正方体内任意转动(忽略摩擦),则此正方体表面积的最小值为.

【考点】
棱柱的结构特征;
棱柱/棱锥/棱台的侧面积、表面积及应用;
基础巩固
能力提升
变式训练
拓展培优
真题演练