1.
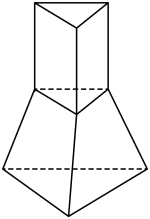
如图，某铁质零件由一个正三棱台和一个正三棱柱组成，已知正三棱柱的底面边长与高均为1cm，正三棱台的下底面边长为2cm，且正三棱台的高为1cm，现有一盒这种零件共重
（不包含盒子的质量），取铁的密度为
．
(1)
试问该盒中有多少个这样的零件？
(2)
如果要给这盒零件的每个零件表面涂上一种特殊的材料，试问共需涂多少
的材料？
【考点】
棱柱的结构特征;
棱台的结构特征;
棱柱/棱锥/棱台的侧面积、表面积及应用;
棱柱、棱锥、棱台的体积;
能力提升
