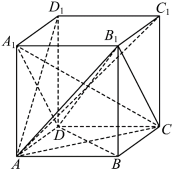
一只蚂蚁从正方体的顶点A处出发，经正方体的表面，按最短路线爬行到达顶点C1位置，则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是( )

1. 一只蚂蚁从正方体 $\text{[math]}$ 的顶点A处出发，经正方体的表面，按最短路线爬行到达顶点C₁位置，则下列图形中可以表示正方体及蚂蚁最短爬行路线的正视图是( )

A. ①② B. ①③ C. ②④ D. ③④

【考点】

棱柱的结构特征;

【答案】

您现在未登录，无法查看试题答案与解析。登录

单选题容易

1. 若干个能确定一个立体图形的体积的量称为该立体图形的“基本量”，已知长方体 $\text{[math]}$ ，下列四组量中，一定能成为该长方体的 “基本量” 的是（）

A. $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的长度 B. $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的长度 C. $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的长度 D. $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 的长度

单选题容易

2. 如图，长方体 $\text{[math]}$ 中， $\text{[math]}$ ，则 $\text{[math]}$ （）

A. 1 B. $\text{[math]}$ C. 2 D. $\text{[math]}$

单选题容易

3. 在透明塑料制成的正方体容器中灌进 $\text{[math]}$ 体积的水，密封后可以任意摆放，那么容器内水面形状可能是：①三角形；②梯形；③长方形；④五边形．
其中正确的结果是（）

A. ①②③ B. ①③④ C. ②③④ D. ①②③④

单选题容易