1.
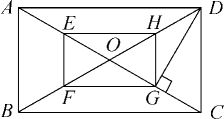
如图1是有两个外开式活动门扇的双开入户铜门.门槛 长为
长为 ,
,  ,
,  分别为左右门扇的底部门宽,且
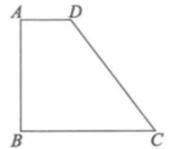
分别为左右门扇的底部门宽,且 , 关上门时,C与D重合.阳光明媚的某天,将两扇门向外开到如图2的位置(平面示意图),这时阳光正好垂直照射向门槛
, 关上门时,C与D重合.阳光明媚的某天,将两扇门向外开到如图2的位置(平面示意图),这时阳光正好垂直照射向门槛 , 因门的遮挡,在门槛上留下三线段
, 因门的遮挡,在门槛上留下三线段 、
、 、
、 , 只有线段
, 只有线段 晒到太阳,且
晒到太阳,且 , 求此时C、D间的距离.
, 求此时C、D间的距离.

【考点】
勾股定理;
矩形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练