1.
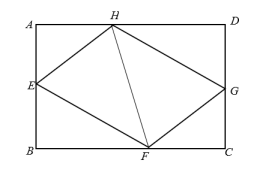
如图,E、F、G、H分别是矩形的边AB、BC、CD、AD上的点,AH=CF,AE=CG,∠EHF=60°,∠GHF=45°.若AH=2,AD=5+ . 则四边形EFGH的周长为( )
. 则四边形EFGH的周长为( )
A.
 B.
B.
 C.
C.
 D.
D.

【考点】
勾股定理;
矩形的判定与性质;
三角形全等的判定-SAS;
基础巩固
能力提升
变式训练
拓展培优