1.
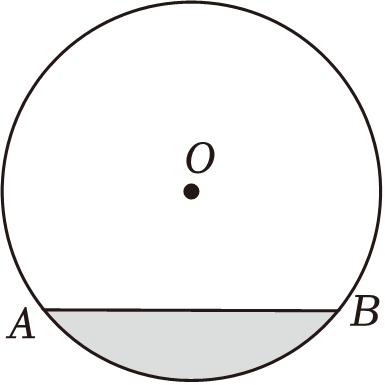
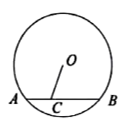
如下图是一个隧道的横截面,它的形状是以点O为圆心的圆的一部分.如果M是 中弦
中弦 的中点,
的中点, 经过圆心O交圆O于点E,并且
经过圆心O交圆O于点E,并且 . 求
. 求 的半径.
的半径.

【考点】
垂径定理的实际应用;
基础巩固
能力提升
变式训练
拓展培优
真题演练