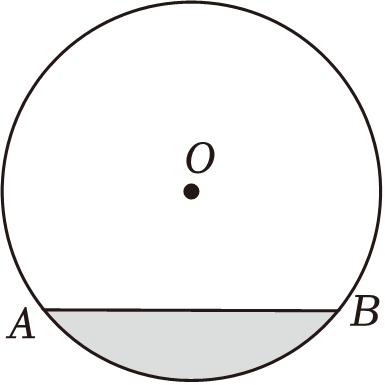
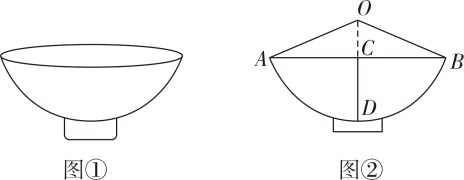
如图①是从正面看到的一个面碗的形状示意图．是⊙O的一部分． D是AB的中点，连接OD，与弦AB交于C．连接OA、OB．已知AB=24cm．碗深CD=8cm，问⊙O的半径OA是多少？

1. 如图①是从正面看到的一个面碗的形状示意图． $\text{[math]}$ 是⊙O的一部分． D是AB的中点，连接OD，与弦AB交于C．连接OA、OB．已知AB=24cm．碗深CD=8cm，问⊙O的半径OA是多少？

【考点】

垂径定理的实际应用;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题普通

1. 石拱桥是我国古代人民勤劳和智慧的结晶（如图1），如图2是根据某石拱桥的实物图画出的几何图形，桥的主桥拱是圆弧形，表示为 $\text{[math]}$ 桥的跨度（弧所对的弦长） $\text{[math]}$ ，设 $\text{[math]}$ 所在圆的圆心为 $\text{[math]}$ ，半径 $\text{[math]}$ ，垂足为 $\text{[math]}$ ，拱高（弧的中点到弦的距离） $\text{[math]}$ ．求这座石拱桥主桥拱的半径．

解答题容易