如图，AB为⊙O的直径，CD是弦，AB⊥CD于点E ， OF⊥AC于点F ， BE＝OF ．

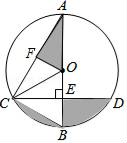
1. 如图，AB为⊙O的直径，CD是弦，AB⊥CD于点E ， OF⊥AC于点F ， BE＝OF ．

(1) 求证：△AFO≌△CEB；

(2) 若BE＝4，CD＝8 $\text{[math]}$ ，求：

①⊙O的半径；

②求图中阴影部分的面积．

【考点】

垂径定理的实际应用; 扇形面积的计算; 三角形全等的判定-AAS;

【答案】

您现在未登录，无法查看试题答案与解析。登录

综合题普通

1. 在 $\text{[math]}$ 中， $\text{[math]}$ ， $\text{[math]}$ ，直线 $\text{[math]}$ 经过点 $\text{[math]}$ ，且 $\text{[math]}$ 于点 $\text{[math]}$ ， $\text{[math]}$ 于点 $\text{[math]}$ ．

综合题普通

综合题普通

综合题普通