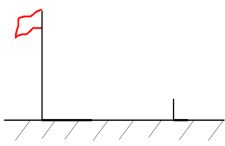
在数学活动课上，老师带领数学小组测量大树的高度．如图，数学小组发现大树离教学楼，大树的影子有一部分落在地面上，还有一部分落在教学楼的墙上，墙上的影子长为，已知此时高的竹竿在水平地面上的影子长，那么这棵大树高度是多少？

1. 小刚和小亮想用测量工具和几何知识测量公园古树 $\text{[math]}$ 的高度，由于有围栏保护，他们无法到达底部 $\text{[math]}$ ，如图，围栏 $\text{[math]}$ 米，小刚在 $\text{[math]}$ 延长线 $\text{[math]}$ 点放一平面镜，镜子不动，当小刚走到点 $\text{[math]}$ 时，恰好可以通过镜子看到树顶 $\text{[math]}$ ，这时小刚眼睛 $\text{[math]}$ 与地面的高度 $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米；同时，小亮在 $\text{[math]}$ 的延长线上的 $\text{[math]}$ 处安装了测倾器（测倾器的高度忽略不计），测得树顶 $\text{[math]}$ 的仰角 $\text{[math]}$ ， $\text{[math]}$ 米，请根据题中提供的相关信息，求出古树 $\text{[math]}$ 的高度．

解答题容易

2. 如图是小明设计用手电来测量某古城墙高度的示意图，点P处放一水平的平面镜，光线从点A出发经平面镜反射后刚好射到古城墙 $\text{[math]}$ 的顶端C处，已知 $\text{[math]}$ ， $\text{[math]}$ ，且测得 $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米，求该古城墙的高度．

解答题容易

3. 如图，路灯（ $\text{[math]}$ 点）距地面8米，身高1.6米的小明从距路灯的底部（ $\text{[math]}$ 点）20米的A点，沿OA所在的直线行走14米到B点时，身影的长度是变长了还是变短了？变长或变短了多少米？

解答题容易

1. 如图，在一个长40m，宽30m的长方形小操场上，王刚从A点出发，沿着A→B→C的路线以3m/s的速度跑向C地.当他出发4s后，张华有东西需要交给他，就从A地出发沿王刚走的路线追赶，当张华跑到距B地 $\text{[math]}$ m的D处时，他和王刚在阳光下的影子恰好重叠在同一条直线上.此时，A处的小旗在阳光下的影子也恰好落在对角线AC上.求：

（1）他们的影子重叠时，两人相距多少米（DE的长）？

（2）张华追赶王刚的速度是多少？

解答题普通

2. 如图，某水平地面上建筑物的高度为AB，在点D和点F处分别竖立高是2米的标杆CD和EF，两标杆相隔52米，并且建筑物AB、标杆CD和EF在同一竖直平面内，从标杆CD后退2米到点G处，在G处测得建筑物顶端A和标杆顶端C在同一条直线上；从标杆FE后退4米到点H处，在H处测得建筑物顶端A和标杆顶端E在同一条直线上，求建筑物的高．

解答题普通

3. 在同车道行驶的机动车，后车应当与前车保持足以采取紧急制动措施的安全距离，如图，在一个路口，一辆长为10m的大巴车遇红灯后停在距交通信号灯20m的停止线处，小张驾驶一辆小轿车跟随大巴车行驶．设小张距大巴车尾xm，若大巴车车顶高于小张的水平视线0.8m，红灯下沿高于小张的水平视线3.2m，若小张能看到整个红灯，求出x的最小值．

解答题普通

1. 如图，为了估计河的宽度，我们可以在河对岸选定一个目标点A，在近岸取点B，使 $\text{[math]}$ 与河岸垂直，在近岸取点C，E，使 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 与 $\text{[math]}$ 交于点D．已测得 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ，则河宽 $\text{[math]}$ 为．

填空题普通

2. 在《数书九章》（宋·秦九韶）中记载了一个测量塔高的问题：如图所示， $\text{[math]}$ 表示塔的高度， $\text{[math]}$ 表示竹竿顶端到地面的高度， $\text{[math]}$ 表示人眼到地面的高度， $\text{[math]}$ 、 $\text{[math]}$ 、 $\text{[math]}$ 在同一平面内，点A、C、E在一条水平直线上．已知 $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米， $\text{[math]}$ 米，人从点F远眺塔顶B，视线恰好经过竹竿的顶端D，可求出塔的高度．根据以上信息，塔的高度为米．

填空题普通

3. 如图，在小孔成像问题中，小孔 O到物体AB的距离是60 cm，小孔O到像CD的距离是30 cm，若物体AB的长为16 cm，则像 CD的长是 cm.

填空题普通

1. 在阳光下，测得一根与地面垂直、长为1米的竹竿的影长为2米．同时两名同学测量一棵树的高度时，发现树的影子不全落在地面上．

(1) 如图1：小明发现树的影子一部分落在地面上，还有一部分影子落在教学楼的墙壁上，量得墙壁上的影长 $\text{[math]}$ 为3.5米，落在地面上的影长 $\text{[math]}$ 为6米，求树 $\text{[math]}$ 的高度．

(2) 如图2：小红发现树的影子恰好落在地面和一斜坡上，此时测得地面上的影长 $\text{[math]}$ 为6米，坡面上的影长 $\text{[math]}$ 为4米．已知斜坡的坡角为 $\text{[math]}$ ，则树的高度为多少米？（结果保留根号）

解答题普通

2. 【项目式学习】

项目主题：学科融合—用数学的眼光观察世界

项目背景：学习完相似三角形性质后，某学校科学小组的同学们尝试用数学的知识和方法来研究凸透镜成像规律．

项目素材：

素材一：凸透镜成像规律： $\text{[math]}$ （ $\text{[math]}$ ）表示凸透镜的焦距， $\text{[math]}$ （ $\text{[math]}$ ）表示物体到凸透镜的距离， $\text{[math]}$ （ $\text{[math]}$ ）表示像到凸透镜的距离，规律如下表

物体到凸透镜距离u	像到凸透镜距离v	像的大小	像的正倒
$\text{[math]}$	$\text{[math]}$	缩小	倒立
$\text{[math]}$	$\text{[math]}$	等大	倒立
$\text{[math]}$	$\text{[math]}$	放大	倒立
$\text{[math]}$	与物同侧	放大	正立