1.
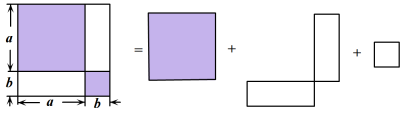
如图①所示是一个长为2m,宽为2n的长方形,沿图中虚线用剪刀均分成四个小长方形,然后按图②的方式拼成一个正方形.

(1)按要求填空:
①你认为图②中的阴影部分的正方形的边长等于______;
②请用两种不同的方法表示图②中阴影部分的面积:
方法1:______
方法2:______
③观察图②,请写出代数式(m+n)2 , (m-n)2 , mn这三个代数式之间的等量关系:______;
(2)根据(1)题中的等量关系,解决如下问题:若|m+n-6|+|mn-4|=0,求(m-n)2的值.
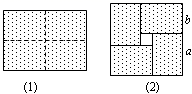
(3)实际上有许多代数恒等式可以用图形的面积来表示,如图③,它表示了______.
【考点】
完全平方公式的几何背景;