1.
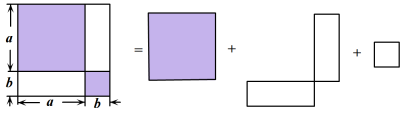
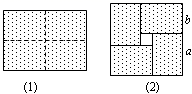
图①是一个长为2m,宽为2n的长方形纸片,将长方形纸片沿图中虚线剪成四个形状和大小完全相同的小长方形,然后拼成图②所示的一个大正方形.

(1)用两种不同的方法表示图②中小正方形(阴影部分)的面积:
方法一: ;
方法二: .
(2)(m+n) , (m−n)
, mn这三个代数式之间的等量关系为___
(3)应用(2)中发现的关系式解决问题:若x+y=9,xy=14,求x−y的值.
【考点】
完全平方公式的几何背景;