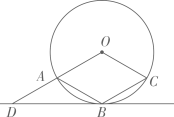
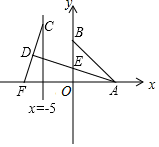
如图，半径为1的在矩形的内部，将圆周12等分，过各等分点作圆的切线，在第一条切线上量取，为图的周长，在第二条切线上量取，在第三条切线上量取，在第四条切线上量取，依此类推，将，，，用光滑的曲线连结，若此时于，于，所在直线恰好经过点，求边的长．

0 返回首页

1. 如图，半径为1的 $\text{[math]}$ 在矩形 $\text{[math]}$ 的内部，将圆周12等分，过各等分点作圆的切线，在第一条切线上量取 $\text{[math]}$ ， $\text{[math]}$ 为图的周长，在第二条切线上量取 $\text{[math]}$ ，在第三条切线上量取 $\text{[math]}$ ，在第四条切线上量取 $\text{[math]}$ ，依此类推，将 $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ ， $\text{[math]}$ 用光滑的曲线连结，若此时 $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 于 $\text{[math]}$ ， $\text{[math]}$ 所在直线恰好经过点 $\text{[math]}$ ，求边 $\text{[math]}$ 的长．

【考点】

切线的性质; 解直角三角形;

【答案】

您现在未登录，无法查看试题答案与解析。登录

解答题困难

基础巩固

能力提升

变式训练

拓展培优

真题演练

换一批

1. 如图，在Rt△ABC中，∠C＝90°，BC＝2，AC＝2 $\text{[math]}$ ．解这个直角三角形．

解答题容易

2. 如图， $\text{[math]}$ 中，已知 $\text{[math]}$ ，点 $\text{[math]}$ 在 $\text{[math]}$ 边上，且 $\text{[math]}$ ，求 $\text{[math]}$ 的长．（结果精确到 $\text{[math]}$ ，参考数据： $\text{[math]}$ ）

解答题容易

3. 根据下列条件，解直角三角形：

（1）在Rt△ABC中，∠C=90°， $\text{[math]}$ ．

（2）在Rt△ABC中，∠C=90°，∠A=60°，c=6．

解答题容易

1. 如图，在 $\text{[math]}$ 中， $\text{[math]}$ 是 $\text{[math]}$ 边上的高， $\text{[math]}$ ．

求：（1）线段 $\text{[math]}$ 的长；

（2） $\text{[math]}$ 的值．

解答题普通

2. 如图，抛物线 $\text{[math]}$ 与x轴交于 $\text{[math]}$ ， $\text{[math]}$ 两点，与y轴交于点C，点P是抛物线上一动点．

（1）求抛物线的解析式；

（2）点P在抛物线上第一象限内时，过点P作 $\text{[math]}$ 轴于点E，交直线 $\text{[math]}$ 于点D，连接 $\text{[math]}$ ， $\text{[math]}$ ，当 $\text{[math]}$ 的面积被直线 $\text{[math]}$ 分成 $\text{[math]}$ 两部分时，求出点P的坐标；

（3）抛物线上是否存在点P，使 $\text{[math]}$ ，当 $\text{[math]}$ 时，请直接写出此时点P的坐标；若不存在，说明理由．

解答题困难

3. 如图，四边形ABCD是矩形，AB＝6，BC＝8，点P从A出发在线段AD上以1个单位/秒向点D运动，点Q同时从点C出发，以1个单位/秒的速度向点A运动，当点P到达点D时，点Q也随之停止运动．

（1）设△APQ的面积为S，点P的运行时间为t，求S与t的函数关系式；

（2）t取几时S的值最大，最大值是多少？

（3）当t为何值时，△APQ是等腰三角形？

解答题普通

1. 如图， $\text{[math]}$ 是 $\text{[math]}$ 的直径， $\text{[math]}$ 是 $\text{[math]}$ 的切线，点 $\text{[math]}$ 为切点，若 $\text{[math]}$ ， $\text{[math]}$ ，则 $\text{[math]}$ 的长为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题容易

2. 为了测量光盘的直径，小帅同学把光盘、三角尺和有刻度的直尺按图所示放置于桌面上．三角尺的斜边与直尺交于点A，光盘分别与直尺和三角尺相切与点B，C．测得 $\text{[math]}$ ，则这张光盘的直径为（）

A. $\text{[math]}$ B. $\text{[math]}$ C. $\text{[math]}$ D. $\text{[math]}$

单选题普通

3. 如图，在平面直角坐标系中，已知 $\text{[math]}$ ，射线 $\text{[math]}$ 满足 $\text{[math]}$ ，点 $\text{[math]}$ 为射线 $\text{[math]}$ 上的一个动点，过 $\text{[math]}$ 作 $\text{[math]}$ 轴于 $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ $\text{[math]}$ 射线 $\text{[math]}$ 交 $\text{[math]}$ 延长线于点 $\text{[math]}$ ，连接 $\text{[math]}$ 并延长交 $\text{[math]}$ 于点 $\text{[math]}$ ，过 $\text{[math]}$ 作 $\text{[math]}$ $\text{[math]}$ 射线 $\text{[math]}$ 交 $\text{[math]}$ 轴于点 $\text{[math]}$ ．

（1）若 $\text{[math]}$ ，则C坐标为；

（2） $\text{[math]}$ 的最大值为．

填空题困难

1. 【问题背景】

已知点 $\text{[math]}$ 是半径为 $\text{[math]}$ 的 $\text{[math]}$ 上的定点，连接 $\text{[math]}$ ，将线段 $\text{[math]}$ 绕点 $\text{[math]}$ 按逆时针方向旋转 $\text{[math]}$ 得到 $\text{[math]}$ ，连接 $\text{[math]}$ ，过点 $\text{[math]}$ 作 $\text{[math]}$ 的切线 $\text{[math]}$ ，在直线 $\text{[math]}$ 上取点 $\text{[math]}$ ，使得 $\text{[math]}$ 为锐角．

(1) 【初步感知】

如图1，当 $\text{[math]}$ 时， $\text{[math]}$ ▲ $\text{[math]}$ ；

(2) 【问题探究】

以线段 $\text{[math]}$ 为对角线作矩形 $\text{[math]}$ ，使得边 $\text{[math]}$ 过点 $\text{[math]}$ ，连接 $\text{[math]}$ ，对角线 $\text{[math]}$ ， $\text{[math]}$ 相交于点 $\text{[math]}$ ．