1.
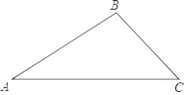
如图所示的衣架可以近似看成一个等腰三角形 , 其中
, 其中 ,
,  ,
,  , 则高
, 则高 约为
约为 .(结果精确到
.(结果精确到 , 参考数据:
, 参考数据: ,
,  ,
,  ).
).

【考点】
解直角三角形;
基础巩固
能力提升
变式训练
拓展培优
真题演练