1.
问题情境:如图1,筒车是我国古代发明的一种水利灌溉工具,假定在水流量稳定的情况下,筒车上的每一个盛水筒都按逆时针做匀速圆周运动,每旋转一周用时120秒.
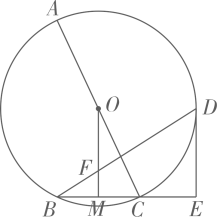
问题设置:如图2,把筒车抽象为一个半径为的
. 筒车涉水宽度
, 筒车涉水深度(劣弧
中点
到水面
的距离)是
.

问题解决:
(1)
求该筒车半径 .
(2)
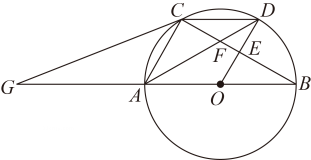
筒车开始工作时,
.
(2)
筒车开始工作时, 上
上 处的某盛水筒到水面
处的某盛水筒到水面 的距离是
的距离是 , 经过
, 经过 秒后,该盛水筒旋转到点
秒后,该盛水筒旋转到点 处.
处.
①求的度数.
②当盛水筒旋转至处时,求它到水面
的距离.
【考点】
勾股定理;
垂径定理;
解直角三角形;