1.
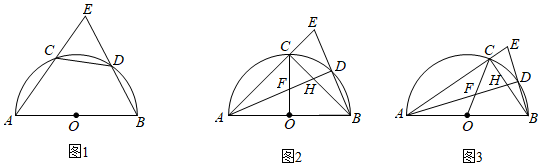
三角形的布洛卡点是法国数学家和数学教育家克洛尔于1816年首次发现,但他的发现并未被当时的人们所注意.1875年,布洛卡点被一个数学爱好者法国军官布洛卡重新发现,并用他的名字命名.如图1,若任意 内一点D满足
内一点D满足 , 则点D叫做
, 则点D叫做 的布洛卡点.如图2,在等腰
的布洛卡点.如图2,在等腰 中,
中, , 点D为
, 点D为 的布洛卡点,
的布洛卡点, ,
,  , 则
, 则 的值为.
的值为.

【考点】
勾股定理;
相似三角形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练