1.
如图,在菱形 ABCD中,∠A=60° ,AB=6.折叠该菱形,使点A落在边BC上的点M 处,折痕分别与边 AB,AD交于点E,F.当点M与点B重合时,EF的长为;当点M的位置变化时,DF长的最大值为.
【考点】
勾股定理;
菱形的性质;
翻折变换(折叠问题);
相似三角形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练




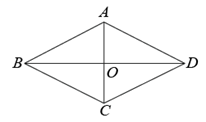


 图13.1
图13.1 图13.2
图13.2 图13.3
图13.3