1.
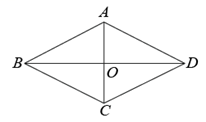
小贤家有一个中国结挂饰, 他想求两对边间的距离, 利用所学知识抽象出菱形  (如图所示), 测得
(如图所示), 测得  , 直线
, 直线  交两对边于点
交两对边于点  , 则
, 则  的长为
的长为  .
.

【考点】
勾股定理;
菱形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练