1.
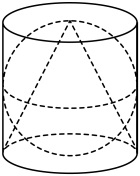
如图所示的图案,是由圆柱、球和圆锥组成,已知球的直径与圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面,则图案中圆锥、球、圆柱的体积 .
.
【考点】
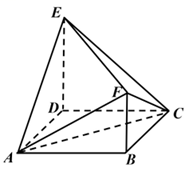
棱柱、棱锥、棱台的体积;
基础巩固
能力提升
变式训练
拓展培优
真题演练