1.
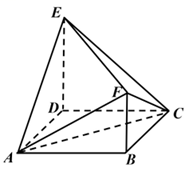
如图,四边形  为正方形,
为正方形,  平面
平面  ,
,  ,记三棱锥
,记三棱锥  ,
,  ,
,  的体积分别为
的体积分别为  ,则( )
,则( )
A.
 B.
B.
 C.
C.
 D.
D.

【考点】
棱台的结构特征;
棱柱、棱锥、棱台的体积;
能力提升
变式训练
拓展培优
真题演练