1.
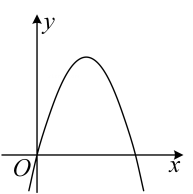
已知抛物线  (如图)和直线
(如图)和直线  .我们规定:当x取任意一个值时,x对应的函数值分别为
.我们规定:当x取任意一个值时,x对应的函数值分别为  和
和  .若
.若  ,取
,取  和
和  中较大者为M;若
中较大者为M;若  ,记
,记  .①当
.①当  时,M的最大值为4;②当
时,M的最大值为4;②当  时,使
时,使  的x的取值范围是
的x的取值范围是  ;③当
;③当  时,使
时,使  的x的值是
的x的值是  ,
,  ;④当
;④当  时,M随x的增大而增大.上述结论正确的是(填写所有符合题意结论的序号)
时,M随x的增大而增大.上述结论正确的是(填写所有符合题意结论的序号)
【考点】
分段函数;
二次函数与一次函数的综合应用;
基础巩固
能力提升
变式训练
拓展培优
真题演练








