1.
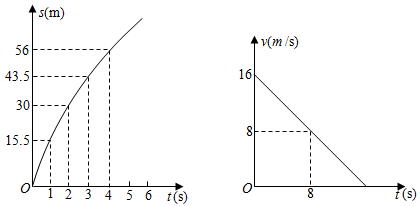
某山区不仅有美丽风光,也有许多令人喜爱的土特产,为实现脱贫奔小康,某村组织村民加工包装土特产销售给游客,以增加村民收入,试销的30天中,该村第一天卖出土特产42千克,为了扩大销量,采取了降价措施,以后每天比前一天多卖出6千克,第x天的售价为y元/千克,y关于x的函数解析式为y=
 ,x为正整数,且第14天的售价为34元/千克,第27天的售价为27元/千克.已知土特产的成本是21元/千克,每天的利润是W元(利润=销售收入﹣成本).
,x为正整数,且第14天的售价为34元/千克,第27天的售价为27元/千克.已知土特产的成本是21元/千克,每天的利润是W元(利润=销售收入﹣成本).
(1)
m=,n=;
(2)
求每天的利润W元与销售的天数x(天)之间的函数关系式;
(3)
在销售土特产的30天中,当天利润不低于1224元的共有多少天?
【考点】
分段函数;
二次函数与一次函数的综合应用;
能力提升
真题演练