1.
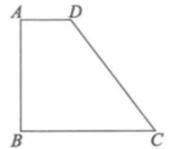
如图1,长方形地砖 中有两个全等的正方形①和②,点E,F分别在
中有两个全等的正方形①和②,点E,F分别在 上,且
上,且 三点共线.点
三点共线.点 分别在
分别在 上,
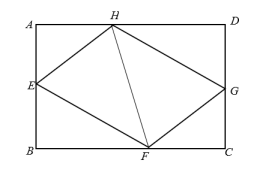
上, , 将两块完全相同的地砖如图2的方式拼接在一起,则阴影部分的面积为( )
, 将两块完全相同的地砖如图2的方式拼接在一起,则阴影部分的面积为( )

A.
62
B.
52
C.
97
D.
87
【考点】
勾股定理;
矩形的判定与性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练