1.
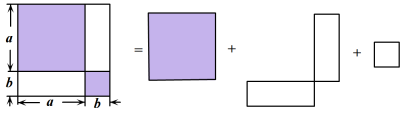
如图,两条线段把正方形ABCD分割出边长分别为a、b的两个小正方形,则利用该图形可以验证因式分解成立的是( )。

A.
 B.
B.
 C.
C.
 D.
D.

【考点】
完全平方公式的几何背景;