1.
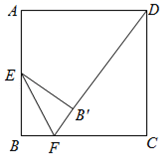
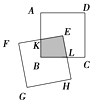
如图,两个边长相等的正方形ABCD和EFGH,正方形EFGH的顶点E固定在正方形ABCD的对称中心位置,正方形EFGH绕点E顺时针方向旋转,设它们重叠部分的面积为S,旋转的角度为θ,S与θ的函数关系的大致图象是( )
A.
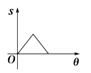 B.
B.
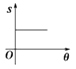 C.
C.
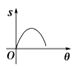 D.
D.

 B.
B.
 C.
C.
 D.
D.

【考点】
全等三角形的判定与性质;
正方形的性质;
基础巩固
能力提升
变式训练
拓展培优
真题演练